Подпишитесь на ютуб канал BayLangTV
Поиск по блогу
Категории
Метки
Свежие записи
Архивы

Обучение многослойного персептрона операции XOR

Обучение многослойного персептрона на примере логической операции XOR.

Обязательно изучите введение в нейронные сети.

В данном примере будем обучать нейронную сеть решать логическую операцию Xor. Xor имеет таблицу истинности.

x1 x2 x1 xor x2
0 0 0
0 1 1
1 0 1
1 1 0

Чтобы решить данную задачу нужно будет создать многослойный персепрон следующего вида:

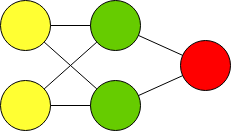
Перед тем как начать работу, установите одну из двух библиотек:

  1. PyTorch и необходимые драйвера
  2. Tensorflow и необходимые драйвера

Решение для PyTorch

Проект perceptron-xor на гитхабе

Подключение библиотек и определение устройства, на котором будут выполняться вычисления: 

import torch
from torch import nn
from torchsummary import summary

# Detect device
tensor_device = torch.device('cuda') if torch.cuda.is_available() else torch.device('cpu')

Подготовка обучающих данных

Перед тем, как начать обучать нейронную сеть, нужно создать обучающий набор данных и нормализировать его. Числа входного и выходного векторов должны быть в пределах от 0 до 1 включительно.

Определяем данные: 

data_train = [
		{ "in": [0, 0], "out": [0] },
		{ "in": [0, 1], "out": [1] },
		{ "in": [1, 0], "out": [1] },
		{ "in": [1, 1], "out": [0] },
]

Это массив вопросов и правильных ответов. Обратите внимание, что входом и выходом являются вектора. Например, вход 2-мерный вектор (0, 0), выход 1-мерный вектор (0).

Сделаем две операции map, которые преобразуют массив data_train отдельно в массив вопросов и ответов. Массив вопросов будет состоять из значения поля "in". Массив ответов будет состоять из значений поля "out". 

# Convert to question and answer
tensor_train_x = list(map(lambda item: item["in"], data_train))
tensor_train_y = list(map(lambda item: item["out"], data_train))

Преобразуем в тензор float32 на устройстве tensor_device. 

# Convert to tensor
tensor_train_x = torch.tensor(tensor_train_x).to(torch.float32).to(tensor_device)
tensor_train_y = torch.tensor(tensor_train_y).to(torch.float32).to(tensor_device)

Выведем на экран полученный результат: 

print ("Input:")
print (tensor_train_x)
print ("Shape:", tensor_train_x.shape)
print ("")
print ("Answers:")
print (tensor_train_y)
print ("Shape:", tensor_train_y.shape)

Должно получится: 

Input:
tensor([[0., 0.],
        [0., 1.],
        [1., 0.],
        [1., 1.]], device='cuda:0')
Shape: torch.Size([4, 2])

Answers:
tensor([[0.],
        [1.],
        [1.],
        [0.]], device='cuda:0')
Shape: torch.Size([4, 1])

Shape означается размерность вектора. Выражение (4, 2) означает, что дан массив из 4х 2-мерных векторов. Или другими словами двумерный массив с 4 строчками и 2 колонками.

На выходе получаем массив из 4х 1-мерных векторов. Обратите внимание, что количество строчек на входе и на выходе одинаковое и равно 4м. У нас в обучающей выборке 4 варианта вопросов и на каждый вопрос есть по одному ответу. В итоге на 4 вопроса, 4 ответа.

Данные подготовили. Сформировали два тензора вопросов и ответов, формата float32. Числа находятся в переделах от 0 до 1.

Можно приступать к созданию нейронной сети.

Создание модели нейронной сети

Архитектура нейронной сети будет следующая.

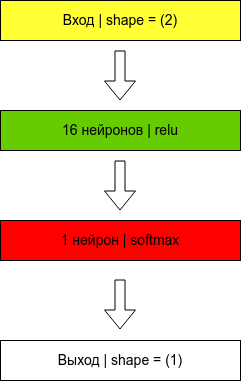
Почему такая? Опытным путем было выяснено, что другие архитектуры неработают. Создание архитектуры нейронной сети напоминает танец с бубном, когда нужно пробовать разные варианты, до тех пор, пока значение функции ошибки не станет минимальным.

Что можно менять:

  • количество слоев.
  • количество нейронов в слое.
  • функции активации.
  • функцию ошибки.

Методом тыка было выяснено, что архитектура нейронной сети должна состоять из 3х слоев.

  1. Входом в нейронную сеть будет являться 2-мерный вектор (x1,x2)
  2. Скрытый слой из 16 нейронов с функцией активации Relu.
  3. Выходной слой из одного нейрона с функцией активации Softmax. В большинстве случаев выход классификатора активируется функцией Softmax. Это важно!
  4. Выходом будет являться 1-мерный вектор, результат операции x1 xor x2

Создаем модель: 

input_shape = 2
output_shape = 1

model = nn.Sequential(
	nn.Linear(input_shape, 16),
	nn.ReLU(),
	nn.Linear(16, output_shape)
)

summary(model, (input_shape,))

Параметры:

  • Размер входного тензора input_shape - 2
  • Размер выходного тензора output_shape - 1
  • Количество нейронов на скрытом слое - 16

Зададим параметры оптимизации для модели: 

# Adam optimizer
optimizer = torch.optim.Adam(model.parameters(), lr=1e-3, betas=(0.9, 0.99))

# mean squared error
loss = nn.MSELoss()

# Batch size
batch_size = 2

# Epochs
epochs = 1000

Параметры:

  • Оптимизатор: Adam
  • Функция ошибка: средне-квадратическая

Получается данная модель создает многослойный персептрон.

Выведем модель на экран: 

summary(model, (input_shape,))

Результат выполнения команды:  

==========================================================================================
Layer (type:depth-idx)                   Output Shape              Param #
==========================================================================================
├─Linear: 1-1                            [-1, 16]                  48
├─ReLU: 1-2                              [-1, 16]                  --
├─Linear: 1-3                            [-1, 1]                   17
==========================================================================================
Total params: 65
Trainable params: 65
Non-trainable params: 0

Число 65 - это количество весов, которые будут в нейронной сети. Это число получается следующим образом:

  1. На входном слое 2 нейрона + 1 нейрон для bias. Итого 3 нейрона
  2. На скрытом слое 16 нейронов. Нужно (2 + 1) * 16 связей, чтобы соединить первый слой со вторым. Получаем число 48. Это число указано в графе параметр
  3. На выходном слое 1 нейрон. Его надо соединить с 16ю нейронами и одним bias нейроном. Итого нужно 17 связей
  4. Получаем всего нужно 48 + 17 = 65 связей и 65 весов для каждой связи.

Обучение нейронной сети

Обучение происходит через метод fit. Передаем в функцию вопросы и правильные ответы. Делаем 250 эпох по 4 обучения в каждой эпохе. 

history = []

# Переместим модель на устройство
model = model.to(tensor_device)

for i in range(epochs):
	
	# Вычислим результат модели
	model_res = model(tensor_train_x)
	
	# Найдем значение ошибки между ответом модели и правильными ответами
	loss_value = loss(model_res, tensor_train_y)
	
	# Добавим значение ошибки в историю, для дальнейшего отображения на графике
	loss_value_item = loss_value.item()
	history.append(loss_value_item)
	
	# Вычислим градиент
	optimizer.zero_grad()
	loss_value.backward()
	
	# Оптимизируем
	optimizer.step()
	
	# Остановим обучение, если ошибка меньше чем 0.01
	if loss_value_item < 0.01:
		break
	
	# Отладочная информация
	if i % 10 == 0:
		print (f"{i+1},\t loss: {loss_value_item}")
	
	# Очистим кэш CUDA
	if torch.cuda.is_available():
		torch.cuda.empty_cache()

Выведем красивый график. Это обязательно, чтобы понять правильно обучилась нейронная сеть или нет. 

import matplotlib.pyplot as plt

plt.plot(history)
plt.title('Loss')
plt.savefig('xor_torch.png')
plt.show()

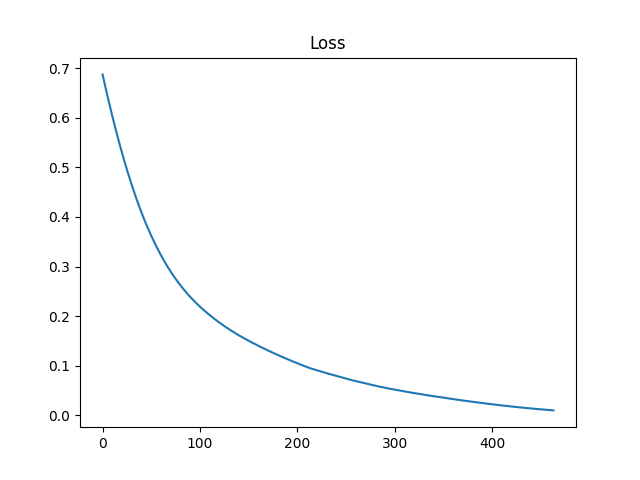
Как видно из графика, ошибка с каждой эпохи стремится к нулю. Делаем вывод, что нейронная сеть прошла обучение успешно.

Внедрение нейронной сети

Напишем небольшой тест для нейронной сети и проверим как она освоила операцию XOR. 

control_x = [
	[0, 0],
	[0, 1],
	[1, 0],
	[1, 1],
]

control_x = torch.tensor(control_x).to(torch.float32).to(tensor_device)

print ("Shape:", control_x.shape)

answer = model( control_x )

for i in range(len(answer)):
	print(control_x[i].tolist(), "->", answer[i].round().tolist())

Выводит результат: 

Shape: torch.Size([4, 2])
[0.0, 0.0] -> [0.0]
[0.0, 1.0] -> [1.0]
[1.0, 0.0] -> [1.0]
[1.0, 1.0] -> [0.0]

Видно, что нейронная сеть отвечает правильно.

Исходный код нейронной сети на TensorFlow 

#!/usr/bin/env python3
# -*- coding: utf-8 -*-

##
# Copyright (с) Ildar Bikmamatov 2022
# License: MIT
# Source:
# https://blog.bayrell.org/ru/iskusstvennyj-intellekt/411-obuchenie-mnogoslojnogo-perseptrona-operaczii-xor.html
##

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Input


# Step 1. Prepare DataSet
data_train = [
	{ "in": [0, 0], "out": [0] },
	{ "in": [0, 1], "out": [1] },
	{ "in": [1, 0], "out": [1] },
	{ "in": [1, 1], "out": [0] },
]


# Convert to question and answer DataSet
data_train_question = list(map(lambda item: item["in"], data_train))
data_train_answer = list(map(lambda item: item["out"], data_train))


# Normalize
data_train_question = np.array(data_train_question, "float32")
data_train_answer = np.array(data_train_answer, "float32")


# Print info
print ("Input:")
print (data_train_question)
print ("Shape:", data_train_question.shape)
print ("")
print ("Answers:")
print (data_train_answer)
print ("Shape:", data_train_answer.shape)

# Wait
print ("Press Enter to continue")
input()


# Step 2. Create tensorflow model
model = Sequential(name='XOR_Model')
model.add(Input(shape=(2), name='input'))
model.add(Dense(16, name='hidden', activation='relu'))
model.add(Dense(1, name='output', activation='softmax'))

# Compile
model.compile(loss='mean_squared_error', 
              optimizer='adam',
              metrics=['accuracy'])
		
# Output model info to the screen		
model.summary()

# Wait
print ("Press Enter to continue")
input()


# Step 3. Train model
history = model.fit(data_train_question, # Input
                    data_train_answer,   # Output
                    batch_size=4,
                    epochs=250,
                    verbose=1)
					
plt.plot( np.multiply(history.history['accuracy'], 100), label='Correct answers')
plt.plot( np.multiply(history.history['loss'], 100), label='Error')
plt.ylabel('%')
plt.xlabel('Epochs')
plt.legend()
plt.savefig('xor_model.png')
plt.show()


# Step 3. Test model
test = [
    [0, 0],
    [0, 1],
    [1, 0],
    [1, 1],
]

test = np.asarray(test)

print ("Shape:", test.shape)

answer = model.predict( test )

for i in range(0,len(answer)):
  print(test[i], "->", answer[i].round())