Введение в нейронные сети
Введение в нейронные сети. Общая постановка задачи. Персептрон. Функции активации нейронов.
Общая постановка задачи
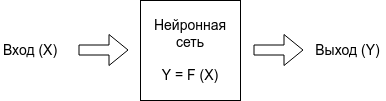
В общем случае задача программирования нейронной сети - это разработать такую нейронную сеть, которая по входу X, будет выдавать правильные ответы Y.
Входом в нейронную сеть могут быть:
- сырые данные, например, звук или фотография.
- либо уже заранее обработанные данные алгоритмом, которые по входу X выдаст признаки (feauture), которые будут передаваться нейронной сети. Данные признаки могут быть определены другой нейронной сетью.
- и т.п.
Выходом могут являться:
- Ответ да или нет.
- Номер категории, к которой принадлежат входные данные.
- Картинка, изображение, звук.
- и т.п.
Задача программиста:
- определить что будет считаться входом в нейронную сеть, а что выходом.
- в каком формате будет принимать нейронная сеть данные.
- структурировать и привести в единую форму входные и выходные данные.
- определить признаки данных, которые могут быть дополнительно поданы на вход в нейронную сеть.
- определить количество слоев нейронной сети.
- определить дополнительные алгоритмы в архитектуре нейронной сети, как отдельные слои.
- создать и разметить DataSet, на котором будет проходить обучение нейронная сеть.
- создать правильную архитектуру нейронной сети.
- обучить нейронную сеть и проверить ее на контрольной выборке.
- внедрить полученную нейронную сеть.
Размеченный DataSet (\(D\)) - это набор данных и известных ответов к ним. По этому датасету обучаются нейронные сети. При этом датасет делится на две части. Обучающий и контрольный. По обучающему датасету нейронная сеть учится, а по контрольному тестируется. Важно, чтобы данные контрольного датасета не попадали в обучающий, иначе нейронная сеть просто заучит правильные ответы.
Правильным результатом считается, когда нейронная сеть наименьше всего ошибается на обоих дата сетах. Берутся ответы нейронной сети и сравниваются с правильными. Чем меньше ошибка, тем лучше работает нейронная сеть.
Функцией ошибки (\(Q\)) называется разница между правильными ответами и ответами, которая выдает нейронная сеть на обучающем и контрольном датасете.
Обучение по размеченному датасету называется обучением с учителем. Есть также другие варианты обучения. Например, без учителя. В данном случае правильные ответы отсуствуют и нейронная сеть должна найти их сама. Эта задача хорошо подходит, например, для нахождения общих признаков на большом количестве данных.
Математикой обучения занимаются алгоритмы популярных библиотек TensorFlow, Keros.
Ахитектурой нейронной сети (\(F\)) - называется цепочка, последовательность слоев этой сети.
Архитектура нейронных сетей может быть разной формы и длины, состоять из нескольких последовательных или паралельных слоев или других цепочек.
Слой - это набор персептронов или определенный алгоритм, который преобразует, по некоторому принципу, входные сигналы p в выходные p'.
Создание архитектуры нейронной сети напоминает конструктор лего, где программист опытным путем подбирает правильный порядок слоев в архитектуре нейронной сети, чтобы она на выходе выдавала правильный результат и значение функии ошибки стремилось к нулю \(Q(F, D) \to 0\)

Каждый слой выполняет определенную функцию. Слои могут отличаться друг от друга.
Примеры слоев:
- простой слой персептронов.
- сверточный слой.
- слой конвертации изображения из двухмерной картинки в одномерный вектор.
- нахождение максимума или минимума.
- фильтрация значения по критерию
- измененя яркости или контрастности.
- удаления или добавление шума.
- Max Pooling и Average Pooling.
- и т.п.
Архитектура нейронной сети может быть иерархической.
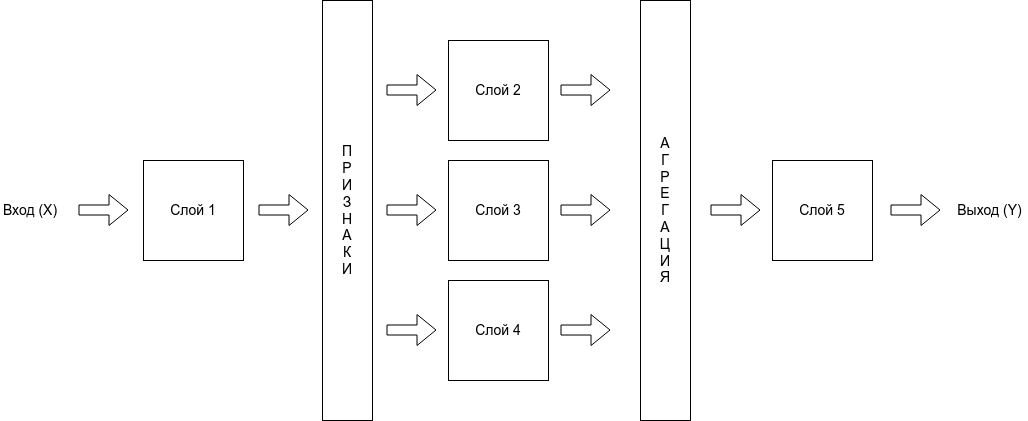
Математическое описание задачи обучения с учителем
Дано:
\(X\) - это входные тестовые данные. Вектор вида \((x_1, x_2, x_3, ... , x_n)\)
\(Y\) - выходные тестовые данные. Вектор вида \((y_1, y_2, y_3, ... , y_k)\)
\(D\) - это обучающая выборка, множество кортежей вида \((X_i,Y_i)\), множество входных значений и ответов к ним (выходных значений), где для каждого \(X_i\) известно \(Y_i\).
\(n\) - длинна вектора \(X\)
\(k\) - длинна вектора \(Y\)
\(m\) - размер выборки, количество кортежей в множестве \(D\)
Требуется:
Найти функцию \(F\), которая \(Y \approx F(X)\)
Обозначим функцию потерь как:
\(L(F,X_i)=|Y_i - F(X_i)|\)
Эта функция означает, насколько ошибается функция \(F\) на конкретном примере \((X_i,Y_i)\).
Функция \(Q\), будет называться функцией ошибки \(F\) на множестве \(D\) и определена как сумма всех значений функции \(L\)
\(Q (F) = \frac{ \sum_{i=1}^{m} L(F,X_i) } {m}\)
Функция \(F\) и ее веса будут найдена при условии \(Q(F) \to 0\)
Есть разные варианты формул ошибки:
Абсолютная ошибка:
\(Q (F) = \frac{ \sum_{i=1}^{m} |Y_i - F(X_i)| } {m}\)
В Tenzorflow loss='mean_absolute_error'
Среднеквадратическая ошибка:
\(Q (F) = \frac{ \sqrt {\sum_{i=1}^{m} (Y_i - F(X_i))^2} } {m}\)
В Tenzorflow loss='mean_squared_error'
Математическая модель нейрона
Нейрон - это атом нейронной сети. У каждого нейрона есть несколько входов и один выход.
Ниже представлена математическая модель одного нейрона.
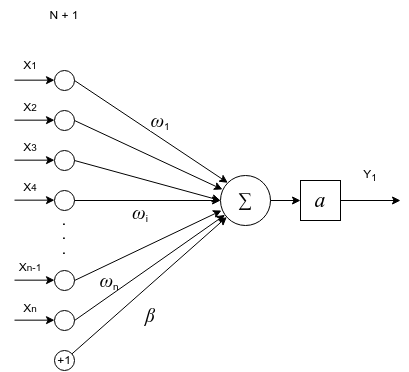
Основная задача нейрона проводить сигнал или гасить его в зависимости от входных значений.
Выходной сигнал нейрона считается как сумма входных значений, умноженная на их веса плюс базис, обработанная функцией активации.
\(y = a(\sum_{i=1}^{n} \omega_i * x_i + \beta)\)
\(a(v)\) - функция активации нейрона. Функция активации нейрона нужна, чтобы определить при каких входных значениях должен активироваться (включаться) нейрон, т.е. проводить сигнал. А при каких нет. Нейрон включается, если достигается нужный уровень сигнала, после этого нейрон передает сигнал дальше. Поэтому функция и называется функцией активации.
\(\omega_i\) - вес нейронной связи. Задает какой входящий сигнал и с какой силой должен учитываться, а какой нет.
\(\beta\) - смещение bias. Это пороговое значение, которое смещает аргумент активационной функции, потому что активация (включение) нейрона может происходит не в точке 0, а в какой-то другой точке. А т.к. функция активации работает в точке ноль, то аргумент нужно сместить по оси x на смещение bias.
Ниже отображена функция активациции со смещением bias. На графике видно, что нейрон будет включаться после аргумента функции больше 2, а не больше 0. Смещение bias в данном случае равно +2.
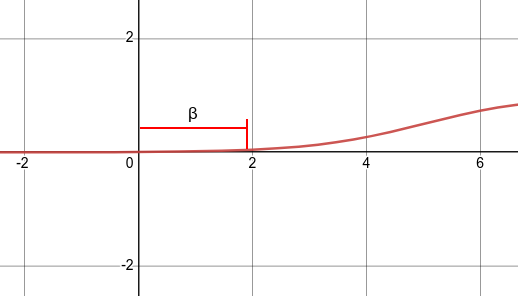
Смещение bias также является входом в нейронную сеть, для которого подбирается свой вес. Этот вес и является смещением. Обычно вес смещения является нулевым весом \(\omega_0\), при входном сигнале равным 1. Получается само смещение вычисляется по формуле \(\beta = \omega_0 *1\)
Тогда формула активации нейрона примет вид:
\(y = a(\omega_0 + \sum_{i=1}^{n} \omega_i * x_i)\)
Это удобно, потому что в данном случае формула принимает одинаковый вид, и для обучения нейрона требуется подобрать кортеж весов \((\omega_0, \omega_1, \omega_2, \omega_3, ... , \omega_n)\)
Функция ошибки и активации являются важными параметрами архитектуры нейронной сети.
Однослойный персептрон
Архитектура нейронной сети состоит из последовательности слоев, которые соединены между собой.
Нейронная сеть состоящая только из входных и выходных слоев называется однослойным персептроном и обозначается упрощенно:
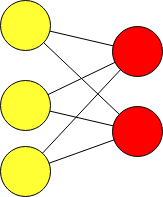
Данная нейронная сеть очень простая. Однослойный персептрон называют более простым термином полносвязный слой. В библиотеке Tensorflow полносвязный слой создается через класс Dense.
Многослойный персептрон
Данный вид нейронной сети имеет следующие названия:
- нейронная сеть с прямой связью
- Feed Forward neural network
- полносвязная сеть
- классификатор
Полносвязная сеть используется очень часто, и хорошо решают задачи на классификацию, например:
- Распознать какая цифра по ее изображению.
- Отличить кошку от собаки.
- Определить какой цветок, по его параметрам (цвет, форма цветка, длинна и т.д.)
- и т.п.
Во сверточных нейронных сетях, полносвязная сеть используется как классификатор на выходе. Сверточная сеть выделяет признаки по картинке и передает ее в полносвязную. А полносвязная уже квалифицирует и выдает ответ.
Многослойный персептрон (полносвязная сеть) - это последовательность полносвязных слоев однослойных персептронов. Основным отличием многослойного персептрона от одногослойного - в наличии одного или более скрытого слоя. Входные и выходные значения соединяются через скрытый слой, а не напрямую, как в однослойном персептроне.
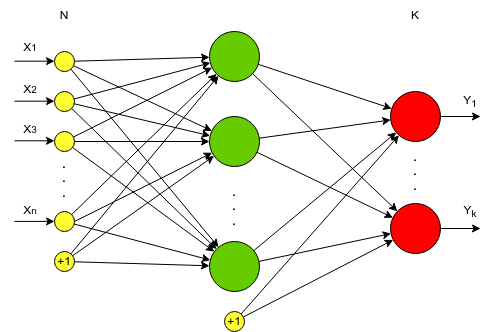
Желтым обозначены входной слой X.
Красным - выходной слой нейронов Y.
Зеленый - это скрытый слой нейронов.
Каждый выход нейрона вычисляется по формуле:
\(p'_j = a(\omega_0 + \sum_{i=1}^{n} \omega_i * p_i)\), где p - это входные значения, а p' - это выходные значения нейрона.
В данной нейронной сети 3 слоя. Входной, скрытый и выходной слой. Данную нейронную сеть часто обозначают упрощенно:
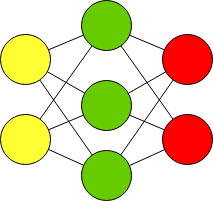
Feed Forward neural network
Текстовая нотация Feed Forward:
ff = [
"Input",
"Dense",
"Output"
];
Многослойный персептрон с более чем одним скрытым слоем называют Deep Feed Forward.
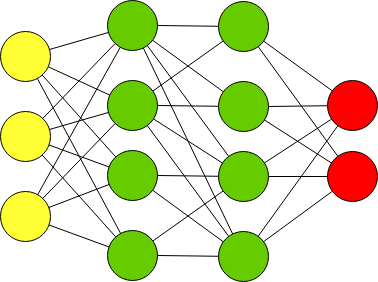
Текстовая нотация Deep Feed Forward:
dff = [
"Input",
"Dense",
"Dense",
"Output"
];
Функции активации нейрона
Пороговая функция активации
\(sign(x) = \begin{cases} -1 & ,x < 0 \\ 0 & ,x = 0 \\ 1 &, x > 0 \end{cases}\)
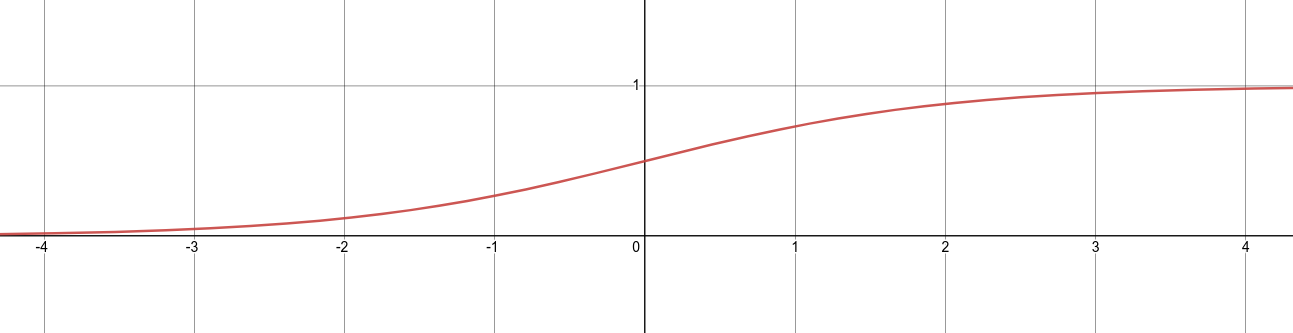
Сигмоида sigm
\(sigm(x) = \frac{1}{1+e^{-x}}\)
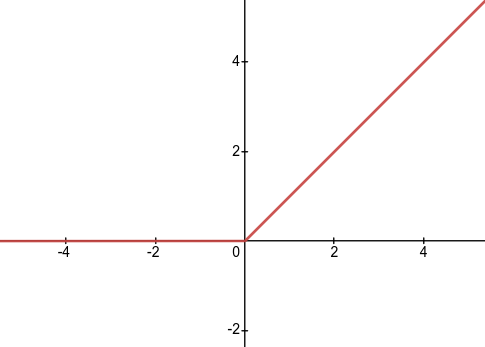
relu
\(relu(x) = max(0,x) = \begin{cases} 0 , x \leq 0 \\ x , x > 0 \end{cases}\)
leaky relu
\(lerelu(x) = \begin{cases} 0.01x & ,x \leq 0 \\ x &, x > 0 \end{cases}\)
Материалы
- Обучение многослойного персептрона операции XOR
- Материалы для самостоятельного изучения нейронных сетей
- Базы датасетов для обучения нейронных сетей
- AIML-4-1 Персептроны
- AIML-4-2 Метод обратного распространения ошибки
- Формулы обратного распространения
- Архитектуры нейронных сетей
- Сервис чтобы строить графики
- Ускорение обучения, начальные веса, стандартизация, подготовка выборки
- Переобучение - что это и как этого избежать, критерии останова обучения
- Функции активации, критерии качества работы НС
- Функции активации. Краткий обзор применений CNN и RNN.
- Playground Tensorflow